Bicycle Laboratorium

Bicycle Laboratorium

E pur si muove

Estimating Competition Rowing Metrics

This blog post provides a brief description of the primary ideas and results that will be found in the paper, "Adaptive smartphone-based sensor fusion for estimating competitive rowing kinematic metrics".

Goal

Competitive rowing highly values boat position and velocity data for real-time feedback during training, racing and post-training analysis. The ubiquity of smartphones with embedded position (GPS) and motion (accelerometer) sensors motivates their possible use in these tasks. We investigate the use of two real-time digital filters to achieve extremely accurate but reasonably priced measures of boat speed and distance per stroke.

Problem

Rowers are primarily concerned with maximizing the speed of their boat and the distance they can cover in each stroke. For this reason, we focus on increasing the accuracy of these two metrics. The GPS from the iPhone samples about once every three seconds, so there is not enough resolution to see what happens within a stroke (which takes about 2 seconds). The accelerometer has an acceptable sampling frequency of 100 Hz, but since rowers are interested in speed and position, it must be integrated or double integrated which introduces a steep low-frequency drift.

Solution

Complementary Filter

The integrated acceleration is high-pass filtered to get rid of the low-frequency drift, but keeps the high-frequency resolution within each stroke. The GPS is low-pass filtered to get rid of any high-frequency noise. These two signals are then summed together.

To get a more accurate result, we apply a linear extrapolation of the previous two GPS position points to get a more accurate prediction between the 0.3 Hz data points.

We use an optimization on each of our 16 data files to generate the optimal low and high cutoff frequencies. We are then able to use the average values over all runs in the filter. With the cutoff frequencies already built in, the filter only needs the previous two data points to operate and runs in real time.

Kalman Filter

The Kalman filter algorithm fuses data collected from different sensors with the outputs of a predictive dynamic physical model to estimate the target time-varying variables of interest, known as states. In our case, the body-fixed longitudinal acceleration of the boat is measured and used as an input to a kinematic model to predict the displacement and speed of the boat along its path. The predictions are then compared with the smartphone GPS-derived distance traveled and speed measurement and the error is used as feedback to adjust the estimation in real time. The Kalman gain can be tuned to balance the sensor and model uncertainty to achieve optimal accuracy.

The smartphone's accelerometer axis is not, in general, parallel to the boat's horizontal travel path. If we want to use the smartphone acceleration for the kinematic model, we must compensate for the sensor misalignment along with varying boat pitch during rowing. This can be done by augmenting the accelerometer's reading (\(\phi_k\)).

Therefore, the kinematic model for the Kalman Filter is as follows:

\begin{align*} d_{k+1} = d_k+ v_k \Delta t \\ v_{k+1} = v_k + (\alpha_{y,k} - \phi_k) \Delta t \end{align*}

This bias term now becomes a new state to be estimated by the filter which will effectively account for drift due to integration error accumulation.

Experimental Validation

We used a differential GPS system (accurate to ~3mm) to define our "ground truth" data. We simultaneously logged data on the differential GPS and the iPhone while a rower performed passes at various speeds up and down a lake. We collected data on two different rower-boat configuration: a single scull boat (one seat) with an elite rower, and a double scull boat (two seats) with a single amateur rower. These offered two very different styles of rowing, so if our filters can perform well on both, then we know they are robust.

Results

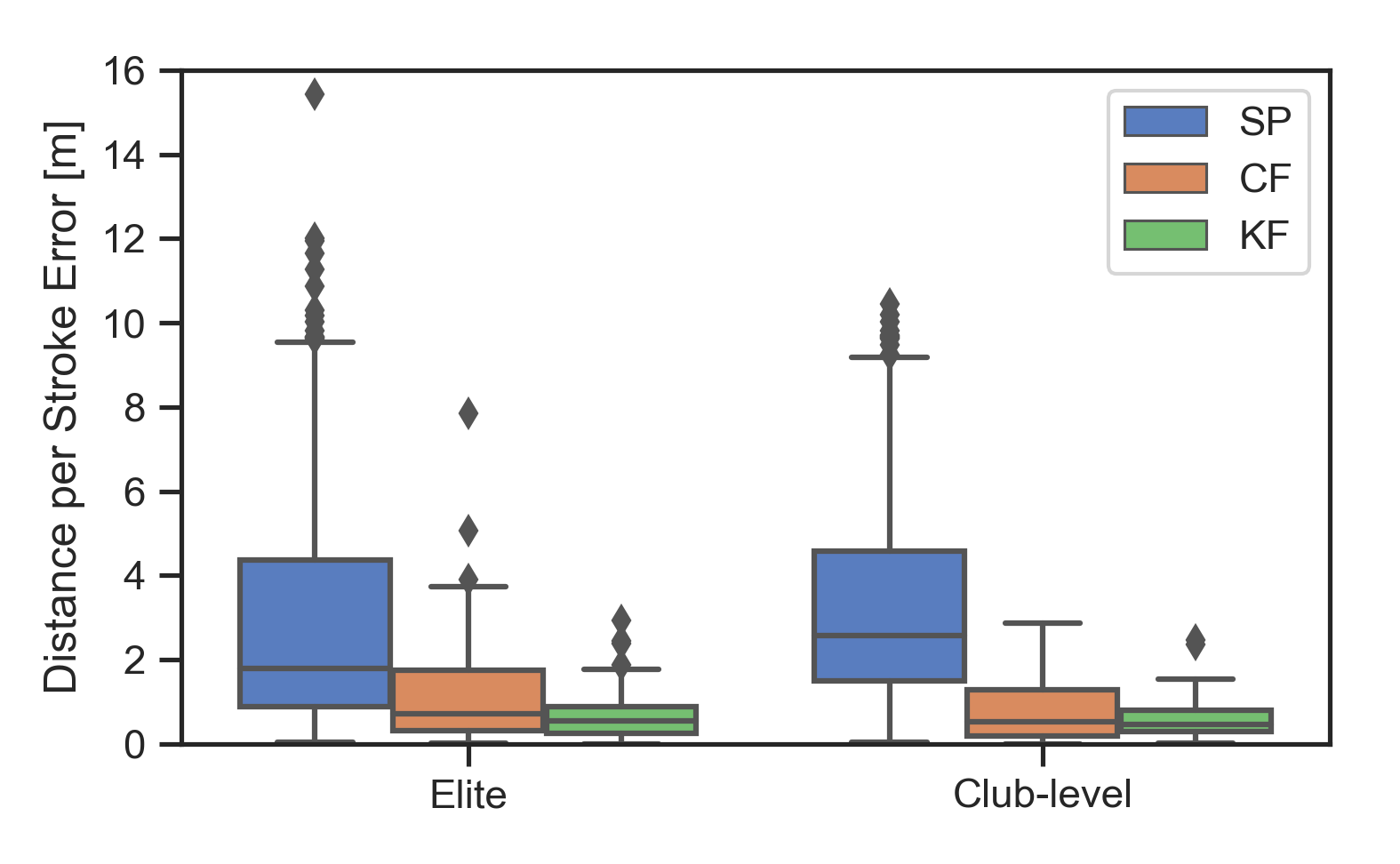
The figure below compares the distance per stroke estimation computed from the smartphone GPS, complementary filter, and Kalman filter through the relative error with respect to the the distance per stroke computed from the differential GPS measurements.

Distance Per Stroke Figure

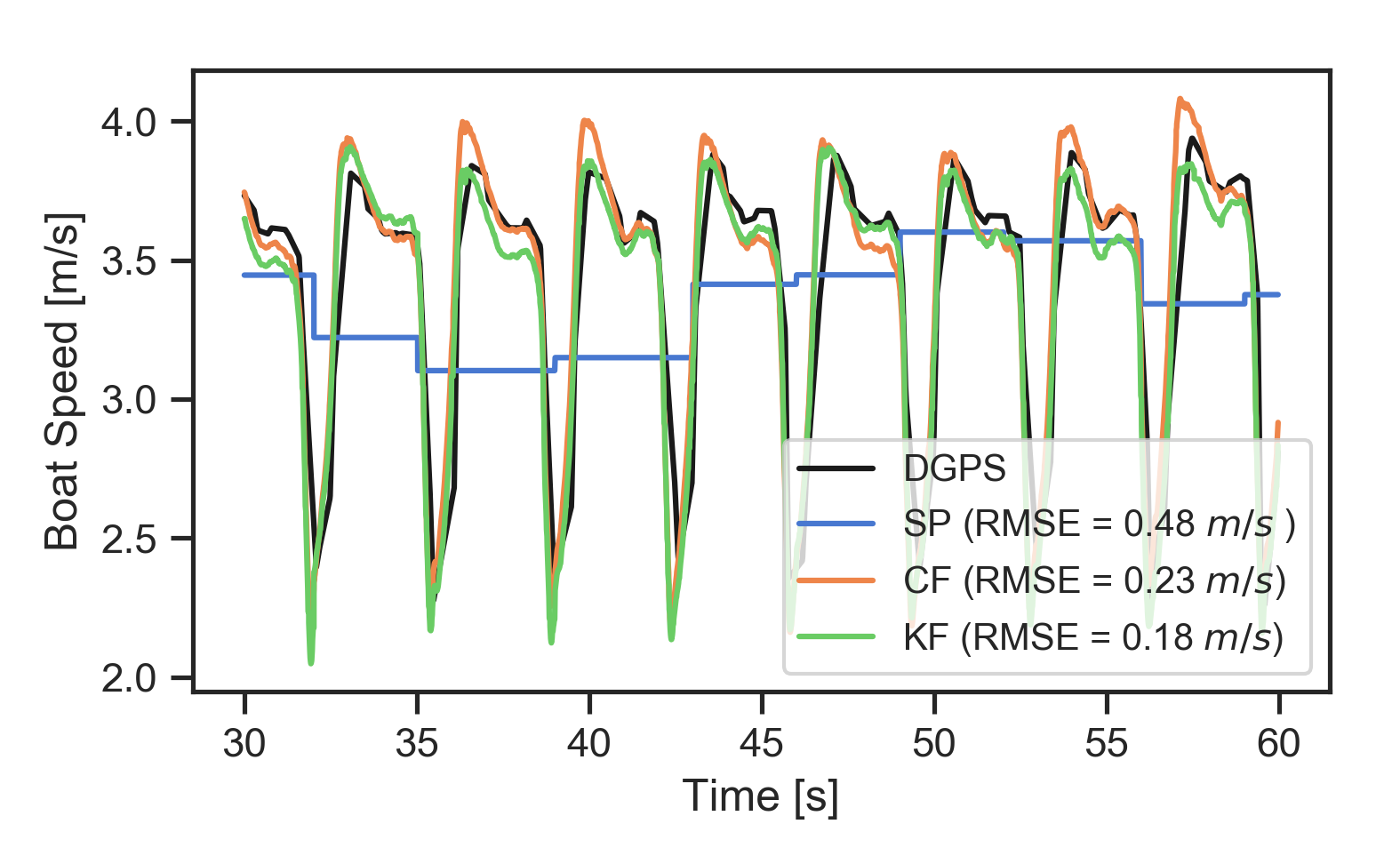
Example boat speed estimates over 30 seconds during a typical trial comparing smartphone GPS derived speed and the complementary filter and Kalman filter outputs against the differential GPS is shown in Figure 2. RMSE is calculated with respect to the sampling rate of the accelerometer, 100 Hz.

Speed Estimation

Discussion

We have presented two methods to estimate the speed and distance per stroke along a rowing boat's path in real time that provide high accuracy and precision from the relatively low accuracy sensors from a single smartphone attached to the boat. These estimates provide an intimate view of the rower's performance. These improved estimates can be used to create a more detailed analysis of the rower's performance. Specifically, we show that the distance per stroke can be estimated to an accuracy of 50~si{centimeter}, which is an improvement over smartphone estimates but still insufficient for detailed stroke-by-stroke level differentiation of boats in a racing event with relatively close elapsed times. Additionally, the inter-stroke view of boat speed that our methods provide are better than any inexpensive commercial on-board boat speed measurement device and compares favorably to very accurate differential GPS systems without the need for more than one GPS receiver.

The complementary filter has a disadvantage in that the filter cutoff frequencies aren't updated to optimal values in real time, and the optimal offline values we make use of do not robustly handle all stroke rates for the two rowers and boats used. This makes the Kalman filter more attractive because the bias term is adaptively updated for every rower and boat. The filter tunes itself. Both filters take time to converge to a steady error from a zero speed start, so the first strokes in a race will produce less accurate results. A future study could look into minimizing the startup time by tuning the filters further, but there is likely a tradeoff in accuracy and precision of the estimations.

Other related information: