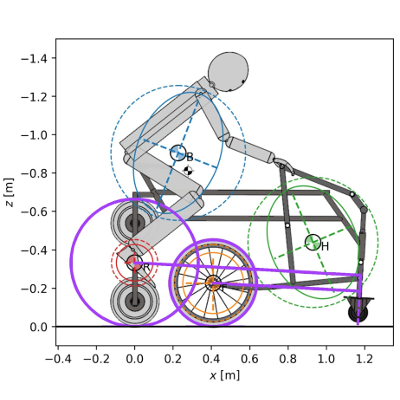
Summary
Our goal with this project is to develop metrics that quantify the handling, i.e. ease of control, of a bicycle or other single track vehicle and using these metrics develop methods for designing bicycles with specified handling characteristics. We have developed an optimization algorithm that can discover bicycle designs which maximize the lateral handling qualities of the vehicle. The algorithm currently produces less-than-intuitive but physically feasible bicycle designs. These methods can likely be extended to any human-machine system design.
| Theme | Bicycle Engineering | Current Researchers | |
| Last Worked On | September 2019 | Past Researchers | Roy Gilboa, Stasia Kubicki, Molly Moritzburke, Anthony Toribio, Shizhao Yang |
| Collaborators | Mont Hubbard, Ronald Hess |
In [Hess2012], we proposed a handling quality metric that can be derived from a bicycle design and its associated human-like controller. Bicycles that have an associated low handling quality metric should be easier to maneuver and control. The handling quality metric can be analytically computed for almost any bicycle design and provides a single value for comparing handling among different designs. In [Moore2012] (Chapter 8: Control), a robust computational method of designing the human-like controller was introduced. These ideas allowed us to frame an optimization problem in which we search for bicycle designs that minimize the handling quality metric. In [Moore2016], we discovered optimal handling designs for various travel speeds by optimizing over four geometric parameters. This created some non-intuitive designs, but they were difficult to realize due to the geometry mismatching with the fixed inertial parameters. We solved this issue in [Moore2019] by developing a constrained optimization problem which enforces consistency and realism in the geometric and inertial parameters. This method produced bicycle designs that can be constructed and tested. We constructed one such bicycle in [Gilboa2019] and showed that the vehicle is realizable and rideable. For this work, we have developed companion open source software [Moore2011] that can create human-like controllers for a broad set of bicycle designs, calculate the handling quality metric, and solve the optimal design problems.
Associated Research Products
Journal articles:
Conference papers:
Conference presentations:
Reports:
- "Optimal Handling Bicycle: Final Design" https://doi.org/10.6084/m9.figshare.12833933.v1
Software:
Blog posts:
Media

Figure taken from [Hess2012] showing the handling quality metrics for an assortment of bicycles.
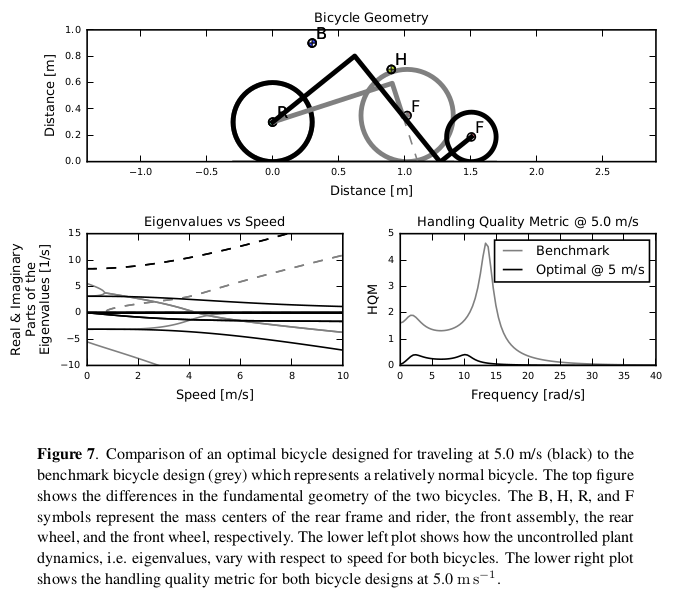
Figure taken from [Moore2016] showing an optimal handling bicycle design for a 5 m/s travel speed compared to the benchmark bicycle from [Meijaard2007].
Image of an early realizable potentiall optimal bicycle. This bicycle design was based on some incorrect analisys and was not constructed.

Fabricated model of optimal bicycle for 3 m/s with rider.
Playlist of videos of some of the bicycles we have constructed.
References
| [Gilboa2019] | (1, 2) R. Gilboa, A. Kubicki, A. Toribio, M. Hubbard, and J. K. Moore, "Practical Realization of a Theoretical Optimal-Handling Bicycle," 2019, p. 11, https://doi.org/10.6084/m9.figshare.9883328.v1. |
| [Moore2019] | (1, 2) J. K. Moore and M. Hubbard, "Expanded Optimization for Discovering Optimal Lateral Handling Bicycles," Padua, Italy, 2019, p. 12, https://doi.org/10.6084/m9.figshare.9942938.v1. |
| [Moore2016] | (1, 2, 3) Moore, Jason, Mont Hubbard, and Ronald A. Hess. "An Optimal Handling Bicycle." In Proceedings of the 2016 Bicycle and Motorcycle Dynamics Conference. Figshare, 2016. https://doi.org/10.6084/m9.figshare.c.3460590.v11. |
| [Moore2012] | J. K. Moore, "Human Control of a Bicycle," Doctor of Philosophy, University of California, Davis, CA, 2012. https://moorepants.github.io/dissertation |
| [Hess2012] | (1, 2, 3) R. Hess, J. K. Moore, and M. Hubbard, "Modeling the Manually Controlled Bicycle," IEEE Transactions on Systems, Man, and Cybernetics - Part A: Systems and Humans, vol. 42, no. 3, pp. 545–557, Feb. 2012, doi: 10.1109/TSMCA.2011.2164244. |
| [Moore2011] | (1, 2) J. K. Moore, HumanControl: Human control of a bicycle. University of California, Davis, 2011. Github: https://github.com/moorepants/HumanControl. |
| [Meijaard2007] | J. P. Meijaard, J. M. Papadopoulos, A. Ruina, and A. L. Schwab, "Linearized dynamics equations for the balance and steer of a bicycle: A benchmark and review," Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, vol. 463, no. 2084, pp. 1955–1982, Aug. 2007. |

